If you have not joined yet, go to your Google Classroom homepage and click "Join" (upper right). Use the code: useuks4
to join.
AMI #5 (AMI #6 for 0B) is due Mon, April 6 by 4 pm. You can send photos through Remind OR upload on Google Classroom Assignment: AMI #5
There is a good set of notes to help with this assignment... currently the first post under Resources on the Classwork section of my Google Classroom.
The AMI packet referred to in the assignment is available under Resources on Classwork on my Google Classroom OR it is on the homepage of this website (scroll down... look for "download")
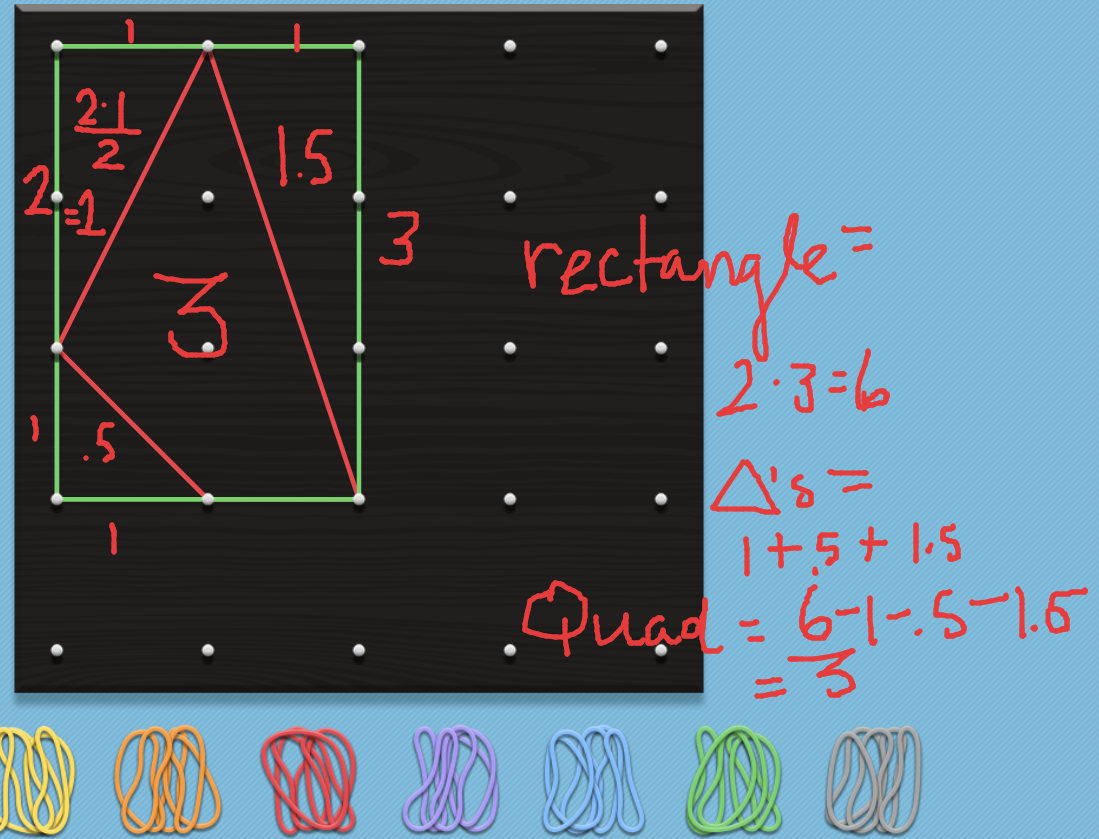
Here is a copy from the Classwork, Assignment, AMI #5:




 RSS Feed
RSS Feed
